Математик 网上买足彩的app,足彩app哪个是正规的 впервые описал движение волн в плоской ленте из плазмы
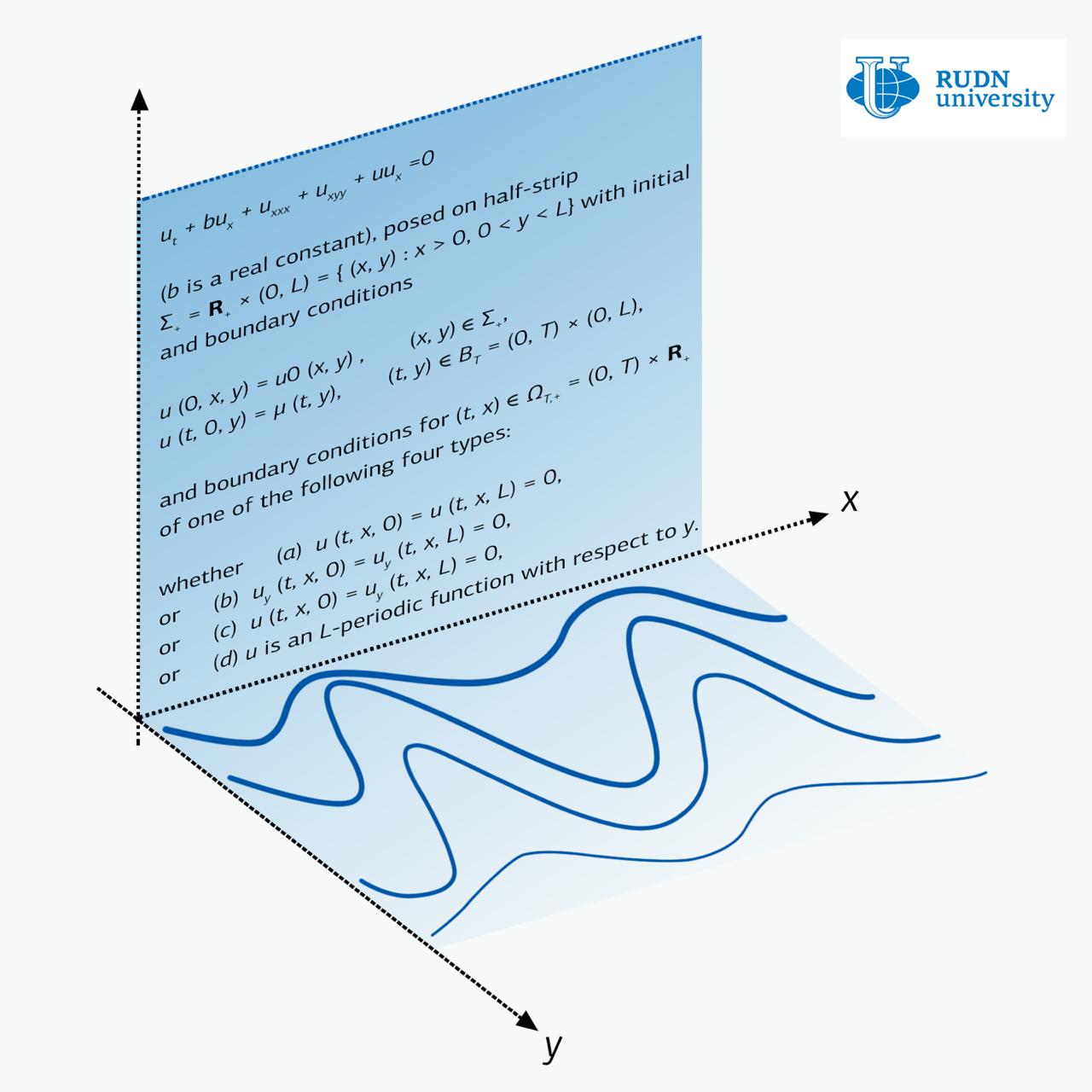
Уравнение Захарова-Кузнецова — это уравнение на одну функцию от двух переменных x и y. С точки зрения физики x - это направление распространения волны, а деформация среды происходит вдоль перпендикулярного направления y. Так, например, выглядит колебание струны гитары - волна бежит по струне, при этом колебания происходят в перпендикулярном относительно бега волны направлении.
Существует большое количество результатов, которые описывают решения уравнений Захарова-Кузнецова в случае, когда по y нет ограничений. Но вопрос распространения волны в полосе — когда y ограничен — до последнего времени был почти не изучен. И это несмотря на то, что у такой постановки задачи есть физический смысл, и, следовательно, потенциальные приложения.
Математики 网上买足彩的app,足彩app哪个是正规的 разобрались с уравнением Захарова-Кузнецова в полосе. Они изучили три основных случая - когда на границе полосы колебаний нет, когда на этой же границе нет тока и когда граничные условия имеют периодическую структуру. Последний случай соответствует распространению волн в среде, структура которой периодична по x.
Во всех этих случаях математикам удалось доказать теоремы существования и единственности решений. Для систем уравнений в частных производных, к которым относится уравнение Захарова-Кузнецова, такие уравнения - большая редкость. Для решений уравнения с начальными условиями в полосе это первые подобные результаты. Плоские потоки плазмы с граничными условиями, которые рассматривали ученые 网上买足彩的app,足彩app哪个是正规的, могут встречаться в физике и астрофизике.
Уравнения Захарова-Кузнецова относятся к более широкому классу уравнений, известных как уравнения типа Кортвега-де Фриза. При изучении этого класса уравнений впервые удалось описать солитоны - волны, форма которых при движении не меняется. Физики рассматривают солитоны как инструмент для работы современных оптических систем передачи данных. Изучение солитонов, которые могут возникать в уравнениях Захарова-Кузнецова, — один из вариантов развития работы, проделанной математиками из 网上买足彩的app,足彩app哪个是正规的.
Статья в журнале Nonlinear Analysis: Real World Applications
Исследователи 网上买足彩的app,足彩app哪个是正规的 вместе с бельгийскими коллегами разработали новые химические соединения, которые могут блокировать образование бактериальных биоплёнок — плотных скоплений микробов, устойчивых к антибиотикам.
Сегодня в составе большинства аналогичных высокочувствительных термометров используют редкоземельные элементы — например, евробий или тербий — из-за их люминесцентных свойств. Исследователи 网上买足彩的app,足彩app哪个是正规的 совместно с учеными Университета ИТМО и Национального научного центра морской биологии им. А.В. Жирмунского предложили альтернативные инновационные нанотермометры на основе металлоорганических каркасов (MOF), в составе которых отсутствуют редкоземельные элементы.
В Москве прошел XXXII Российский национальный конгресс «Человек и лекарство» для специалистов здравоохранения. Исследование Анны Абрамовой, аспиранта кафедры общей клинической фармакологии 网上买足彩的app,足彩app哪个是正规的, отмечено дипломом победителя. Анна изучала тему «Роль олокизумаба в снижении воспаления и смертности у пациентов с COVID-19.